We argue that “quality scores” for software packages must take into account the number and quality of the package’s dependencies. We suggest an algorithm that does exactly that and we provide an open-source implementation.
Table of Contents
Introduction
People in the software industry are becoming more aware of the problems that come from depending on third-party open-source software, and it appears necessary to lower the quantity and increase the quality of third-party software dependencies.
Among the tools that can help with increasing the quality of open-source software are quality scores like the OSSF Scorecard project. Each software package is given a number representing how reliable and trustworthy it is, helping developers increase the quality of their dependencies and giving package maintainers an incentive to adopt best practices.
This score however is only computed based on the package itself, not the packages it depends on. This is a serious limitation to the value of such scoring, because a developer who wants to use a package has no choice but to install the package’s dependencies as well, meaning that the quality and quantity of these dependencies should be taken into account when deciding whether or not to install a package. Existing mechanisms like the OSSF Scorecard do not provide this information, and this the gap we attempt to brigde here.
The only other similar attempt we are aware of is the “Proof-of-Diligence algorithm” by Stacklok which is very recent, seems quite complex to evaluate, and does not seem to have been made public.
One naive solution would be for the developer to look up the score of each dependency of the package by themselves. This process is so tedious that most developers won’t go through the trouble. But even if they do check all the scores for a package’s dependencies, it might still be unclear how to use these scores to decide whether or not to install the package, or to compare it with others.
In the following, we refer to the intrinsic score of package $p$, written as $s_p$, as the score representing the “quality” of $p$ independently of its dependencies. Typically, this is the OSSF Scorecard score of the package or a similar quality score. We propose a new score, the aggregated score of $p$, written as $s^\prime_p$, which considers the quality and quantity of $p$’s dependencies. Both scores (intrinsic and aggregated) are real numbers between 0 and 1.
We denote by $D_p$ the set of direct dependencies of $p$, and by $\bar{D}_p$ the set of all dependencies of $p$, both direct and transitive:
$$ \bar{D}_p = D_p \cup \bigcup_{q ~ \in ~ D_p} \bar{D}_q $$What we expect from an aggregated score is that it favors packages with few and high-quality dependencies. This means that it should increase when a package removes dependencies or when the intrinsinc score of it or some of its dependencies increases.
A First Attempt: Minimum Score
The simplest aggregated score is probably to take the lowest score among $p$ and its dependencies. That is, formally:
$$ \min(\{ s_p \} \cup \{s_q ~|~ q \in \bar{D}_p\}) $$The upside of this aggregated score is that it requires no arithmetic, so it can be easily evaluated by a human just by looking at the intrinsinc score of all dependencies.
The downside of this aggregated score is that, while it will never decrease when removing dependencies or increasing the score of a dependency, it’s not guaranteed to increase either. This is not ideal, as removing dependencies or increasing the score of any dependency does make the situation better, so we would like the aggregated score to go higher and not to stay the same.
Multiplying Scores
We then suggest another aggregated score where we multiply the intrinsic score of $p$ with that of all its dependencies.
$$ s'_p = s_p \times \prod_{q \in \bar{D}_p}{s_q} $$Because scores are numbers between 0 and 1, adding a new dependency will always reduce the aggregated score, and increasing the intrinsic score of either $p$ or any of its dependencies will always increase the aggregated score.
This new definition for an aggregated score also makes more sense: the purpose of scoring systems like OSSF Scorecard is to represent the probability that a package turns into an attack vector, and the purpose of this aggregated score we try to build is to represent the probability that installing it introduces an attack vector, either from the package itself or from one of its dependencies.
Because a high score is supposed to represent a low chance of turning malicious, assume that $1- s_p$ represents the probability that $p$ turns malicious at some point. Then, the probability that $p$ never turn malicious is $s_p$, and the probability that neither $p$ nor any of its dependencies ever turn malicious is the aggregated score we just suggested:
$$ s_p \times \prod_{q \in \bar{D}_p}{s_q} $$
With this definition, a package with an intrinsic score of 7/10 and 3 dependencies with scores 5/10, 7/10 and 9/10 would have an aggregated score of 2.2/10.
Mapping Scores to Probability of Maliciousness
In practice however, while intrinsic scores like the OSSF Scorecard are linked to the probability of never turning malicious, they are not meant to be interpreted directly as this probability. In other words, a package with an OSSF Scorecard of 5/10 does not have a 50% chance of becoming malicious.
We propose the following function for mapping an intrinsic score of a package to its “trustworthiness”, meaning the probability of this package to never turn malicious:
$$ s \mapsto 1 - 0.2 \times \left( 1 - \frac{\log(1 + (k-1)s)}{\log(k)} \right) $$
where $k$ is some parameter for which we suggest a value of 60.
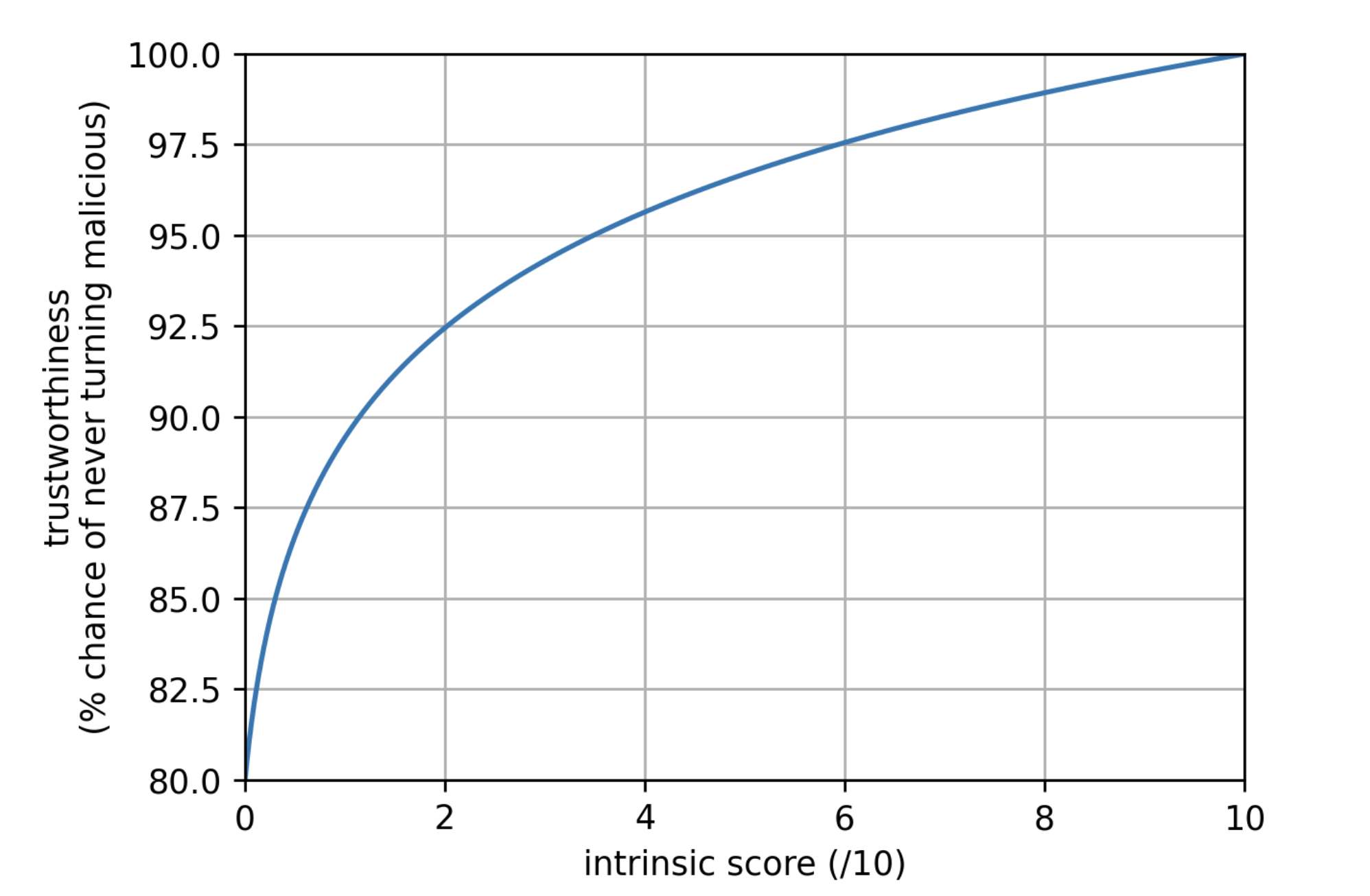
plot of the suggested trustworthiness function
This function has no other rationale than being simple to express and compute, and (we think) aligns with how most people will interpret the score of a package. In the remainder of this document we call this function the “trusworthiness function”, represented by $f$, which can be replaced by any stricly increasing continous function from $[0, 1]$ to either $[0, 1]$ itself or a interval of it. $t_p = f(s_p)$ is called the intrinsic trustworthiness of package $p$.
We denote by $f^{-1}$ the inverse of $f$. However since we will apply some arithmetic on trustworthiness values, we may end up with an aggregated trustworthiness that is out of the codomain of $f$, and thus cannot be inverted via $f^{-1}$. We then define $\tilde{f}^{-1}$ as the following surjection from $[0, 1]$ to itself:
$$ \tilde{f}^{-1}(y) = \begin{cases} 0 &\text{if } y \leq \min(f([0, 1])) \\ 1 &\text{if } y \geq \max(f([0, 1])) \\ f^{-1}(y) &\text{if } y \in f([0, 1]) \\ \end{cases} $$We then suggest a new definition for the aggregated score of $p$:
$$ \begin{align*} s'_p &= \tilde{f}^{-1}(t'_p) \\ &= \tilde{f}^{-1}( t_p \times \prod_{q \in \bar{D}_p}{t_q} ) \\ &= \tilde{f}^{-1}( f(s_p) \times \prod_{q \in \bar{D}_p}{f(s_q)} ) \\ \end{align*} $$This definition is very similar to the previous one, but it is more “sound” in the way it uses probability theory.
Reusing our previous example, and using the trustworthiness function suggested above, with this new definition, packages with an instrinsic score of 5/10, 7/10 and 9/10 would have a respective instrinsic trustworthiness of about 96.7%, 98.3% and 99.5%, leading to an aggregated trustworthiness for our package $p$ of about 92.9%, corresponding to the same aggregated score of about 2.2/10.
Incentivizing the Removal of Transitive Dependencies
Another property we may expect from an aggregated score is to favor packages whose dependencies are mostly direct instead of transitive: packages should favor dependencies which have few dependencies themselves. The rationale here is that package maintainers probably audit their direct dependencies more that their transitive ones, and that it is easier for a package maintainer to remove a problematic dependency if it is direct than if it is transitive. Transitive dependencies are what make managing dependencies so difficult in the first place, so we aim to promote shallow dependency trees.
In order to achieve this, we suggest to amplify the effect a dependency has on the aggregated score of a package depending on how deep it is in the dependency graph of this package.
We suggest a new definition for the aggregated trustworthiness $t^\prime_p$ of a package as the product of two factors, it’s intrinsic trustworthiness $t_p$ and it’s “transitive” trustworthiness $\hat{t}_p$ , where the transitive trustworthiness $\hat{t}_p$ is the product of some power $e > 1$ (we suggest $e = 1.5$) of the aggregated trustworthiness of each direct dependency of $p$:
$$ \begin{align*} t'_p &= t_p \times \hat{t}_p \\ &= t_p \times \prod_{q \in D_p} (t'_q)^e \end{align*} $$Let’s apply this definition on an example package $p$ having 3 direct dependencies $q_1$, $q_2$ and $q_3$, all 3 of them having no dependencies. Because they have no dependencies, their transitive trustworthiness is equal to 1 and their aggregated trustworthiness is equal to their intrinsic trustworthiness. The transitive trustworthiness of $p$ is then equal to
$$ t'_p = t_p \times {t_{q_1}}^e \times {t_{q_2}}^e \times {t_{q_3}}^e $$Now let $q_4$ be a dependency of $q_1$ with $q_4$ having no dependencies. The transitive trustworthiness of $q_1$ changes from 1 to ${t_{q_4}}^e$, and as a consequence the aggregated trustworthiness of $q_1$ changes from $t_{q_1}$ to $t_{q_1} \times {t_{q_4}}^e$. The aggregated trustworthiness of $p$ becomes then:
$$ t_p \times \left( t_{q_1} \times {t_{q_4}}^e \right)^e \times {t_{q_2}}^e \times {t_{q_3}}^e $$which is equal to
$$ t_p \times {t_{q_1}}^e \times {t_{q_2}}^e \times {t_{q_3}}^e \times {t_{q_4}}^{e^2} $$In Appendix B we show that this generalizes to computing the aggregated trustworthiness $t^\prime_p$ of $p$ as the product of $t_p$ and, for each dependency $q$ of $p$ (both direct and transitive), for each path $u$ in the depencency graph from $p$ to $q$, $t_q$ raised to the power of $e^{|u|}$ where $|u|$ is the length of $u$, that is:
$$ t_p \times \prod_{ \substack{q ~ \in ~ \bar{D}_p\\u ~\in~ \text{paths}(p, q)} } {t_q}^{e^{|u|}} \label{eq-1}\tag{1} $$Where $\text{paths}(p, q)$ is the set of all paths from $p$ to $q$ in the dependency graph (modeled as a directed acyclic graph). See Appendix B for a proof of this equivalence.
Let’s apply it on a slightly more complex graph:
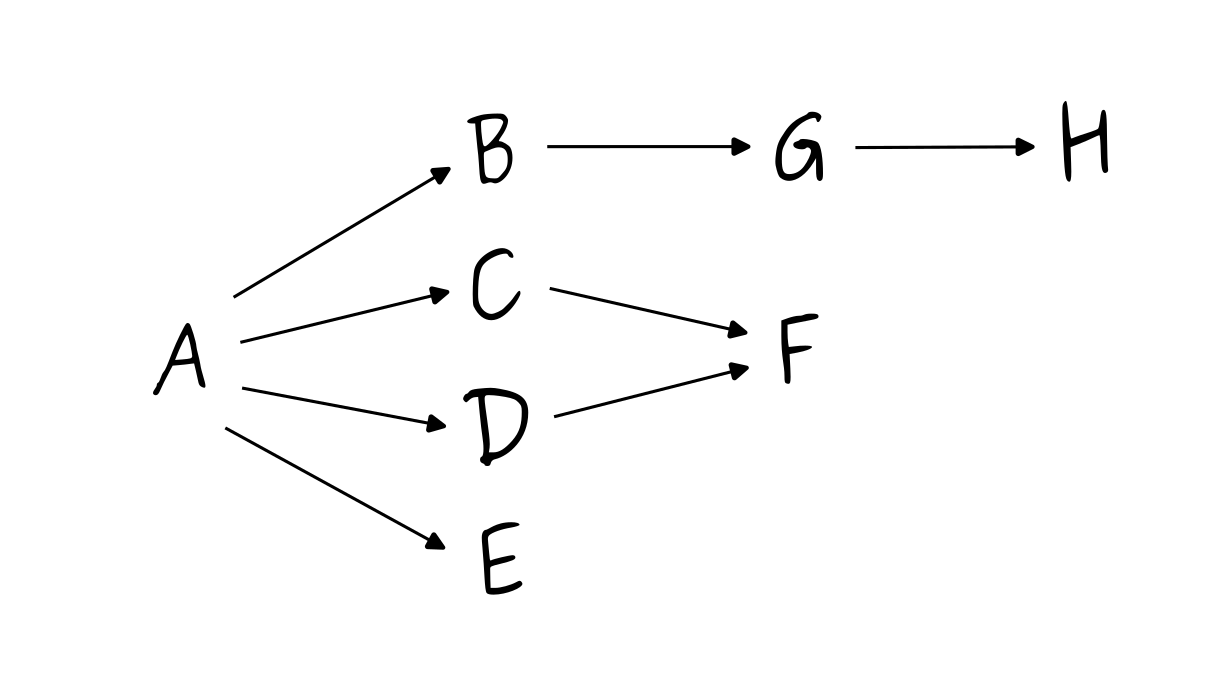
the dependency graph
Here, the aggregated trustworthiness $t^\prime_A$ of $A$ is:
$$ t_A \times {t_B}^e \times {t_C}^e \times {t_D}^e \times {t_E}^e \times {t_F}^{2e^2} \times {t_G}^{e^2} \times {t_H}^{e^3} $$Note that this definition has the benefit of offering some opportunities for caching: for each dependency of a package, if one had already computed the aggregated trustworthiness for this dependency and saved the transitive trustworthiness of this dependency, then one can skip all the computation for the sub-graph starting from this dependency.
Conclusion
We have designed an algorithm which assigns a score to any software package representing how installing this package and all of its dependencies will affect one’s exposure to malicious packages and other forms of supply-chain attacks.
This algorithm only requires each package to have an “instrinsic score”, an assumption which is already satisfied by existing tools like the OSSF scorecard but can be replaced by other similar tools. While definitely being a heuristic instead of a natural law, our algorithm is based on a sound probabilistic reasonning and produces results that match the intuition. The algorithm favors packages with a small number of trustworthy dependencies, and also favors packages with shallow dependency graphs compared to deep ones. Finally, it is efficient to compute since computations can be skipped for parts of the graph that were already visited during previous evaluations.
An open source (Apache 2 license) implementation is available at https://github.com/DataDog/aggregated-dependency-score
Acknowledgements
Thanks to Christoph Hamsen for bringing the “Proof-of-Diligence algorithm” by Stacklok to our attention.
Appendix A: inverse of $f$
$$ \begin{align*} t &= 1 - 0.2 \times \left( 1 - \frac{\log(1 + (k-1)s)}{\log(k)} \right) \\ 1 - \frac{\log(1 + (k-1)s)}{\log(k)} &= (1-t)/0.2 \\ \frac{\log(1 + (k-1)s)}{\log(k)} &= 1 - (1-t)/0.2 \\ \log(1 + (k-1)s) &= (1 - (1-t)/0.2) \log(k) \\ 1 + (k-1)s &= k^{1 - (1 - t)/0.2} \\ s &= \frac{1 - k^{1 - (1 - t)/0.2}}{1 - k} \end{align*} $$Appendix B: Proof of the Equivalence of Two Different Expressions for the Aggregated Score
Given the final definition of the aggregated trustworthiness:
$$ \begin{align*} t'_p &= t_p \times \hat{t}_p \\ &= t_p \times \prod_{q \in D_p} (t'_q)^e \end{align*} $$we show that it implies that
$$ t'_p = t_p \times \prod_{ \substack{q ~ \in ~ \bar{D}_p\\u ~\in~ \text{paths}(p, q)} } {t_q}^{e^{|u|}} \label{eq-1}\tag{1} $$where $\text{paths}(p, q)$ is the set of all paths from $p$ to $q$ in the dependency graph and $|u|$ is the length of path $u$.
First, we note that it is trivially true for packages that have no dependencies, since both expressions degenerate to simply $t^\prime_p = t_p$ when $D_p = \empty$. It is also trivially true for packages that only have direct dependencies as both expressions degenerate to
$$ t_p \times \prod_{q \in D_p} {t_q}^e $$Finally, we use a proof by induction by showing that, if the statement holds true for all packages which dependency graph only has paths of length at most $n$, then it is true for all packages wich dependency graph only has paths of length at most $n+1$.
Assume then than the two expressions are equivalent for all packages which dependency graph only has paths of length at most $n$. Let $p$ be a package which depencency graph only has paths of length at most $n+1$. It is easy to show that all the direct dependencies of $p$ have a dependency graph with paths of length at most $n$: if one direct dependency $q$ of $p$ had a path $u$ in its dependency graph with a length greater than $n$, then the dependency graph of $p$ would have a path of length greater than $n+1$, being the concatenation of the path from $p$ to $q$ and the path $u$. The statement we are proving is then true for all direct dependencies of $p$.
The aggregated trustworthiness of $p$ is, by definition,
$$ t_p \times \prod_{q \in D_p} (t'_q)^e $$First, we do a relabelling from $q$ to $r$, as it will make the proof easier to follow later:
$$ t_p \times \prod_{r \in D_p} (t'_r)^e $$Since the equivalence we are trying to prove is true for all direct dependencies $r$ of $p$, we can replace $t^\prime_r$, leading to
$$ t_p \times \prod_{r \in D_p} \left( t_r \times \prod_{ \substack{q ~ \in ~ \bar{D}_r\\u ~\in~ \text{paths}(r, q)} } {t_q}^{e^{|u|}} \right)^e \label{meeting-point}\tag{2} $$Now we start from the other expression
$$ t_p \times \prod_{ \substack{q ~ \in ~ \bar{D}_p\\u ~\in~ \text{paths}(p, q)} } {t_q}^{e^{|u|}} \tag{1} $$and show that it is, too, equivalent to $(2)$.
In $(1)$, the product is over all dependencies $q \in \bar{D}_p$. We split it between direct dependencies in $D_p$ and non-direct dependencies in $\bar{D}_p \setminus D_p$:
$$ t_p \times \prod_{\substack{r ~ \in ~ D_p\\u ~\in~ \text{paths}(r, q)}} {t_r}^{e^{|u|}} \times \prod_{ \substack{q ~ \in ~ \bar{D}_p \setminus D_p\\u ~\in~ \text{paths}(p, q)} } {t_q}^{e^{|u|}} $$For each direct dependency $r \in D_p$ of $p$, there is only one path from $p$ to $r$ and its length is 1, so we can simplify the first product and get
$$ t_p \times \prod_{r ~ \in ~ D_p} {t_r}^e \times \prod_{\substack{ q ~ \in ~ \bar{D}_p \setminus D_p \\ u ~\in~ \text{paths}(p, q) }} {t_q}^{e^{|u|}} $$Then, for every non-direct dependency $q \in \bar{D}_p \setminus D_p$ of $p$,
for every path $u \in \text{paths}(p, q)$ from $p$ to $q$,
there is a unique direct dependency $r \in D_p$ of $p$
and a unique path $v \in \text{paths}(r, q)$ from $r$ to $q$
of length $|v| = |u| - 1$
such that $u$ is the concatenation of the path of length one from $p$ to $r$ and and $v$.
The converse is true as well,
creating a one-to-one mapping between $\text{paths}(p,q)$
and the set
The expression $(1)$ is then equivalent to
$$ t_p \times \prod_{r ~ \in ~ D_p} {t_r}^e \times \prod_{q ~ \in ~ \bar{D}_p \setminus D_p} ~ \prod_{r \in D_p} ~ \prod_{v \in \text{paths}(r, q)} {t_q}^{e^{|v| +1}} $$Which we can reorder to
$$ t_p \times \prod_{r \in D_p} \left( t_r \times \prod_{ \substack{q ~ \in ~ \bar{D}_r\\u ~\in~ \text{paths}(r, q)} } {t_q}^{e^{|u|}} \right)^e $$