Une démonstration intuitive du théorème de Pythagore

Le théorème de Pythagore dit que, dans un triangle rectangle, le carré de la longueur de l’hyphoténuse est égal à la somme du carré de la longueur des deux autres côtés.

Avant de démontrer ce théorème, on va rappeler la signification de certains des termes : un triangle est dit « rectangle » quand il a un angle droit, c’est à dire un angle de 90 degrés, autrement dit un quart de tour. L’hypothénuse est le côté d’un triangle rectangle qui est à l’opposé de l’angle droit. Enfin, le carré d’un nombre est ce nombre multiplié par lui même, par exemple le carré de $2$ est $2×2=4$. On appelle cela le « carré » d’un nombre parce que c’est la surface d’un carré dont la longueur est ce nombre.

Si on note $c$ la longueur de l’hypothénuse et $a$ et $b$ celle des deux autre côtés, alors le théorème de Pythagore s’écrit :

$$ a^2 + b^2 = c^2 $$

Plutôt que de donner la preuve tout de suite, on va essayer de voir comment on peut trouver la preuve en réfléchissant.

On veut montrer que $a^2 + b^2 = c^2$. On rapelle que $a^2$ est « la surface d’un carré de côté $a$ ». On est donc tenté de dessiner des carrés à partir de chacun des côtés du triangle, pour faire apparaître les trois quantités dont il est question dans le théorème, c’est à dire $a^2$, $b^2$ et $c^2$.

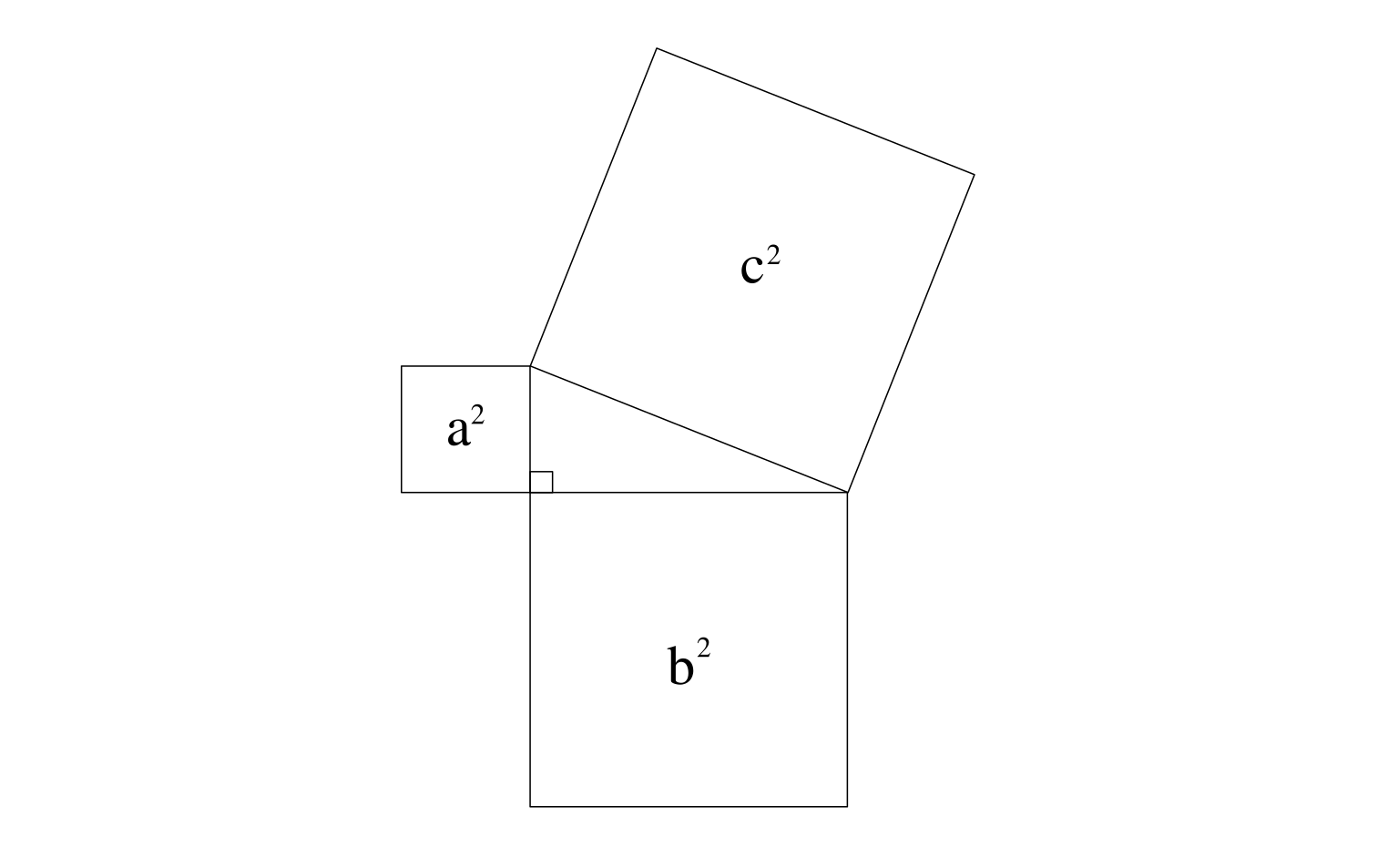
Est-ce qu’il y a un moyen de démontrer le théorème de Pythagore en commençant par là ? Oui, mais ça n’est pas la direction qu’on va prendre, et celle qu’on va prendre donne sans doute la preuve la plus simple et la plus facile à comprendre.

Une des choses qui fait que dessiner les trois carrés précédents ne donne pas une preuve facile, c’est qu’on ne voit pas trop comment on va pouvoir représenter l’addition de $a^2$ et $b^2$ de cette manière. Chacun des carrés est facile à dessiner séparément, mais c’est difficile de représenter $a^2 + b^2$.

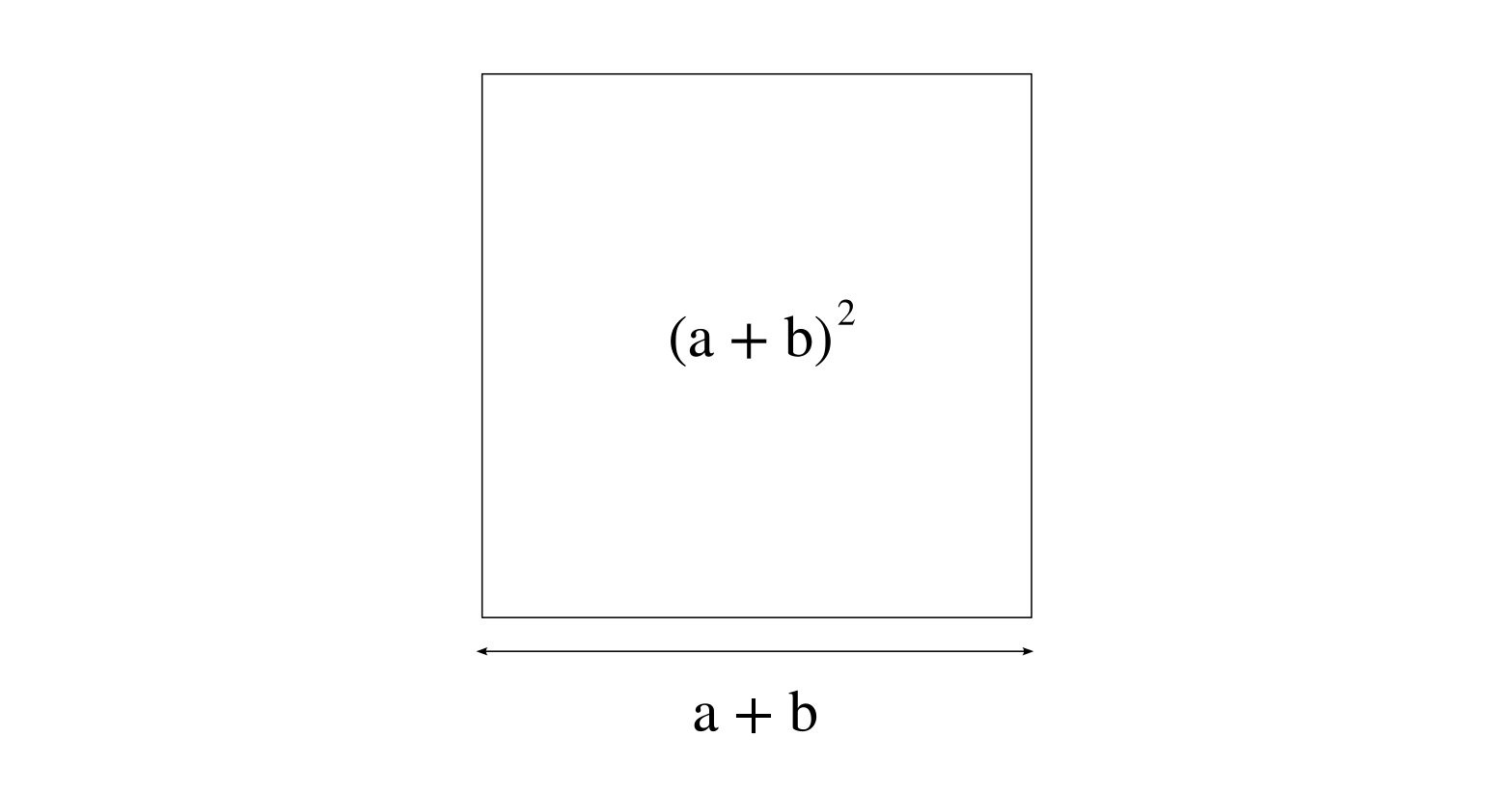
Ce qu’on sait représenter facilement en revanche, c’est $(a + b)^2$ : c’est la surface d’un carré dont les côtés sont de longueur $a +b$. Ça n’est pas exactement la même chose que $a^2 + b^2$, mais ça s’en rapproche: $(a + b)^2$ est égal $a^2 + b^2 + 2ab$, c’est une des « identités remarquables » qu’on apprend au lycée. On peut le re-démontrer rapidement (en notant $ab$ la multiplication de $a$ et $b$ pour que ce soit plus lisible) :

$$ \begin{align*} (a + b)^2 &= (a + b) × (a + b) \\ &= \left(a × (a+b)\right) + \left(b × (a+b)\right) \\ &= a^2 + ab + ba + b^2 \\ &= a^2 + b^2 + 2ab \end{align*} $$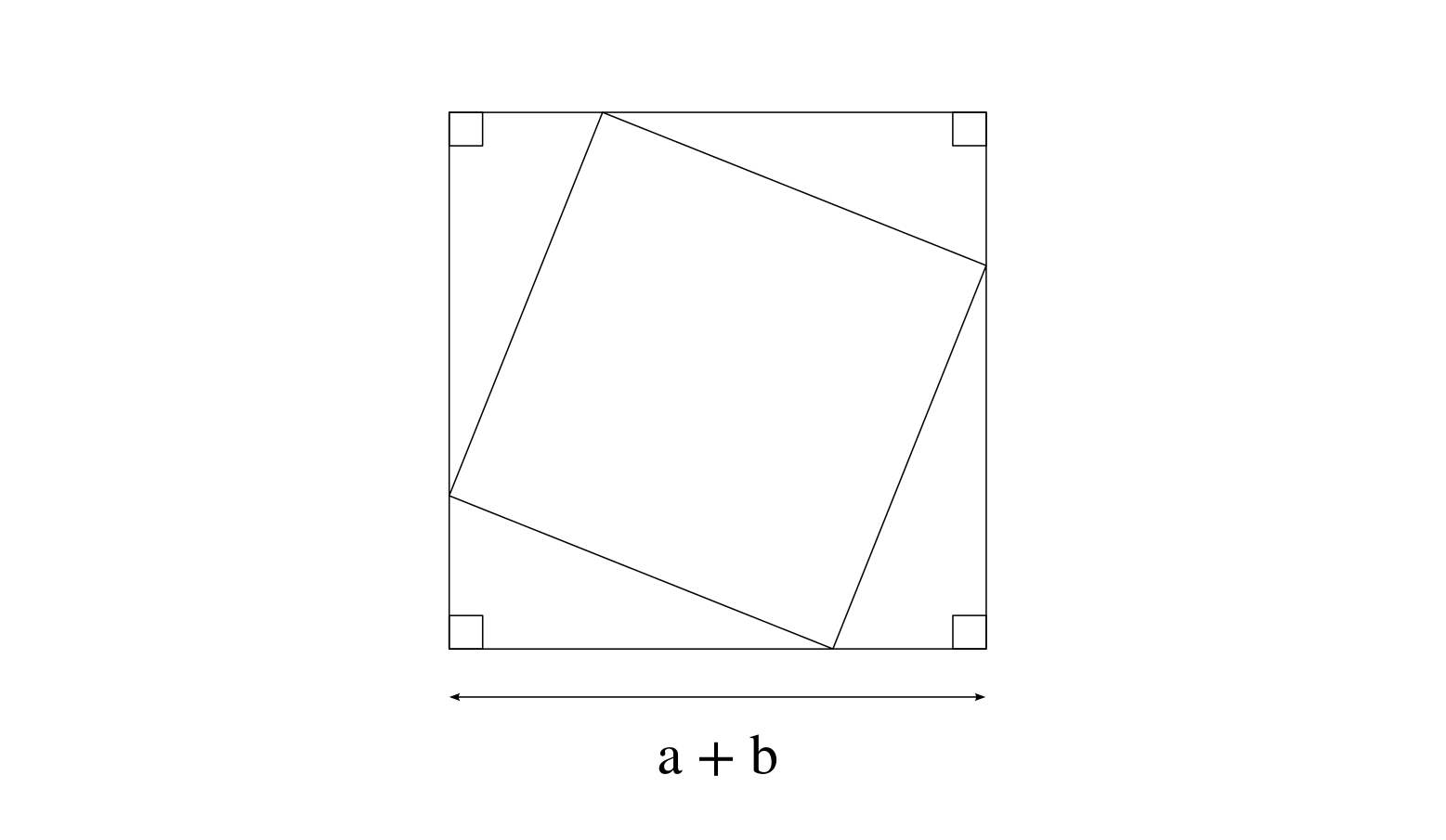

Or non seulement on sait représenter facilement $(a + b)^2$, mais on peut le faire avec notre figure de départ, le triangle rectangle ! Il suffit mettre bout-à-bout le côté de longeur $a$ d’un triangle avec le côté de longueur $b$ d’une copie de ce triangle. Pour que les deux côtés soient alignés, il faut que le deuxième triangle soit tourné de 90 degrés, ce qui est parfait parce qu’on peut répéter cela trois fois et revenir à notre point de départ, avec un carré de longeur $a + b$ composé de quatres copies de notre triangle rectangle.

Comme on vient de le voir, la surface du carré qu’on vient de construire est de $(a + b)^2$ qui peut aussi s’écrire $a^2 + b^2 + 2ab$. Mais on a une autre manière d’exprimer la surface de ce carré en faisant la somme des surfaces des parties qui le compose : c’est quatre fois la surface de notre triangle rectangle de départ, plus la surface du carré central (le carré légèrement tourné) formé par les quatre hypothénuses.

D’ailleurs, il faut qu’on prouve que les deux carrés qu’on a construit sont effectivement des carrés. Pour ça, il suffit de montrer que leurs quatre angles sont droits et que leurs quatre côtés sont de la même longeur.

Pour le grand carré, tous les côtés ont la même longueur $a + b$, et les quatre angles sont les angles droits des quatre triangles rectangle. Pour le carré central, les quatre côtés ont la même longeur $c$, et les angles sont droits parce qu’ils sont formés par le même côté de deux copies de notre triangle rectangle après que l’une des copies soit tournée de 90°. On a donc bien deux carrés.

La surface du carré central est de $c^2$, ce qui nous intéresse particulièrement parce que $c^2$ apparaît dans le théorème de Pythagore mais n’apparaissait pas encore dans nos calculs.

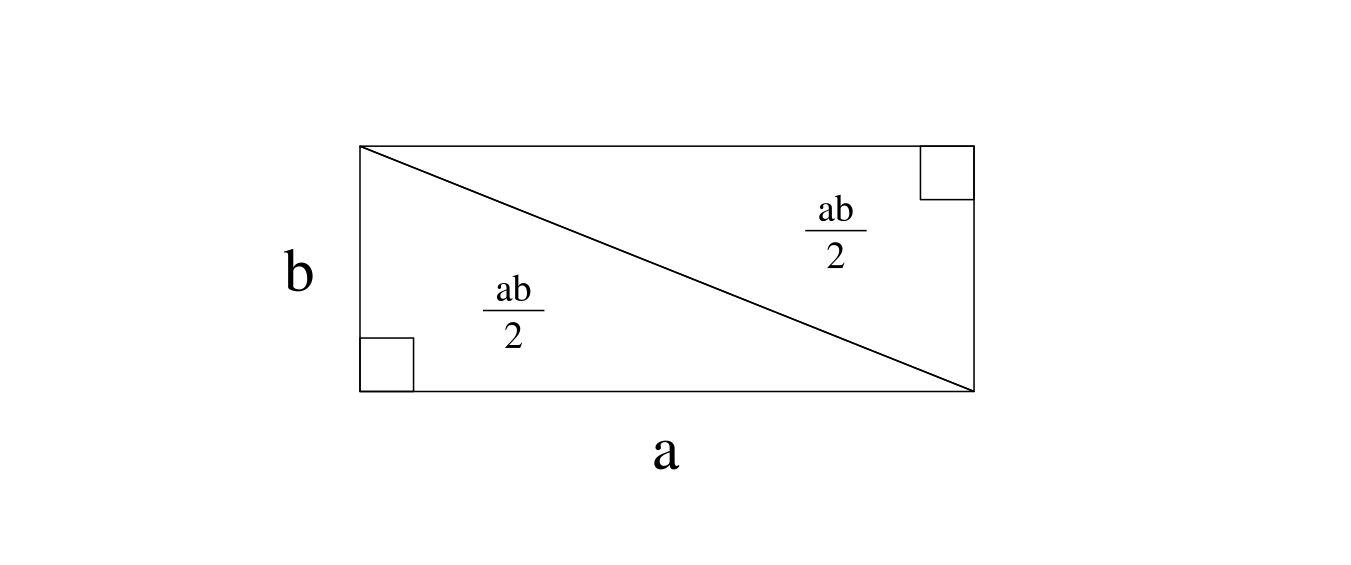
La surface de chacun des triangles rectangle est de $ab/2$. C’est un résultat très connu et qu’on peut facilement démontrer en montrant qu’avec deux triangles rectangles identiques, on peut former un rectangle de côtés $a$ et $b$, et donc de surface $a \times b$, en tournant un des triangles d’un demi tour. C’est d’ailleurs pour cela que ce type de triangle est dit « rectangle » : c’est la moitié d’un rectangle.

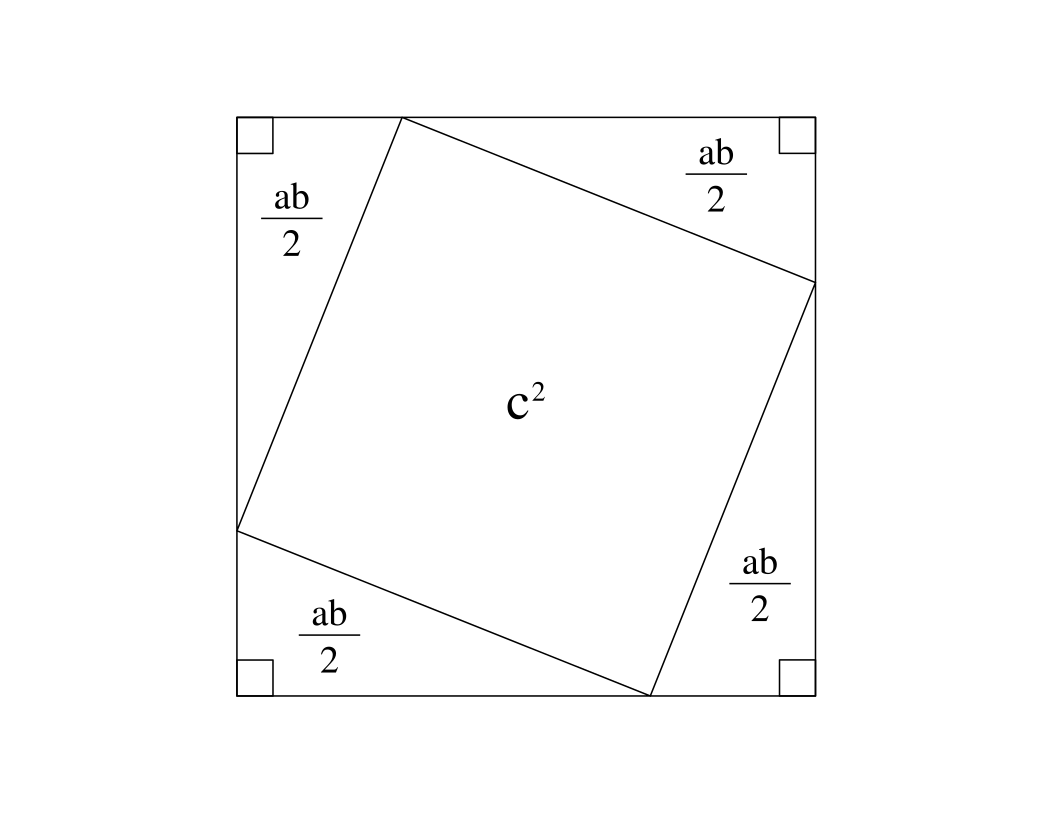
La surface de notre grand carré est donc aussi égale à $4×(ab/2) + c^2$ qu’on peut simplifier en $2ab + c^2$.

Comme on a obtenu deux expressions différentes pour la surface du grand carré, ces deux expressions sont égales, et on peut écrire

$$ a^2 + b^2 + 2ab = 2ab + c^2 $$

Cette technique, de trouver deux expressions différentes d’une même quantité, est utilisé très souvent dans les preuves mathématiques.

Il suffit d’enlever $2ab$ de chaque côté pour obtenir le théorème de Pythagore :

$$ a^2 + b^2 = c^2 $$

Autres resources sur Internet

Sur YouTube: